Introduction
사용자(및 아이템)의 규모가 커짐으로 인하여 모델의 크기가 지속적으로 증가한다.
많은 연산 시간과 메모리 비용이 필요하기 때문에 실사건 플랫폼에 대규모 모델을 적용하기 어렵다.
Knowledge distillation(KD, 지식 증류)는 성능을 유지하면서 모델의 크기를 줄이기 위해 RS에 적용됐다.
여기서 KD는 이전에 학습된 대형 모델(교사)로부터 지식을 이전하여 새로운 소형 모델(학생)의 학습을 가속화하는 전략이다.
이 프로세스의 핵심 아이디어는 교사 모델이 예측한 소프트 라벨이 학습 세트에 명시적으로 포함되지 않은 엔티티(즉, 사용자 및 항목) 간의 숨겨진 관계를 드러내 학생 모델의 학습을 가속화하고 향상시킨다는 것이다.

기존의 방법에는 한계가 있다.
학생 모델의 학습이 교사의 예측 결과에 의해서만 유도되어 교사에게 저장된 지식을 충분하게 활용하지 못한다.
또한, Figure 1을 보면 교사의 추천 목록은 두 item에 대해 비슷한 수준의 선호도를 가지고있음을 보여준다. 하지만 해당 교사의 잠재 지식에는 사용자가 두 item의 다른 측면을 더 좋아한다는 자세한 정보가 포함되어있다.
해당 논문에서는 이러한 잠재 지식을 활용하여 학생 모델의 성과를 더 향상시킨다고 한다.
한 번에 하나의 item을 고려하는 point-wise 방식으로 교사의 예측에서 지식을 추출한다.
이는 여러 항목을 동시에 고려하지 않아 교사 모델이 예측한 순위 순서를 정확하게 유지하는데 한계가 있다.
본 논문은 교사 모델에서 저장된 잠재 지식(a)와 교사의 예측에서 다시 드러난 지식(b)를 모두 증류하는 새로운 RS용 Knowledge Distillation framework인 DE-RRD를 제안한다.
Contribution
1. 교사 모델에서의 잠재 지식 증류(DE)
2. 교사 모델의 예측으로부터 Relaxed Ranking Distillation(RRD)
3. 통합 프레임워크(DE-RRD)
Problem Formulation
여기선 implicit feedback에 대한 Top-K 추천에 초점을 맞춰 진행된다.
\( \mathcal{U}, \mathcal{I} \)는 각각 user, item 집합을 의미한다.
CF 정보(사용자와 아이템 간 implicit feedback interaction)이 주어지면 binary matrix \( R \in \{0, 1 \}^{| \mathcal{U} | \times | \mathcal{I} | } \)를 구축한다.
여기서 R은 사용자가 아이템과 상호작용이 존재할경우 1, 아닐 경우 0을 갖는다.
지식 증류(KD)의 과정은 다음과 같다.
1. learning parameter가 많은 교사 모델을 binary label이 존재하는 training set으로 학습시킨다.
2. learning paramter가 적은 학생 모델을 교사 모델의 도움을 받아 binary label을 추가하여 학습시킨다.
여기서 KD의 목표는 적은 수의 learning paramter로도 교사의 추천 성능을 유지할 수 있는 프레임워크를 설계하는 것이다.
DE-RRD
DE-RRD는 다음과 같이 구성되어있다.
1. 교사의 잠재 지식을 직접 전달하는 Distillation Experts(DE)
2. 교사의 예측에서 드러난 지식을 item 간 순위를 직접 고려해 전수하는 Relaxed Ranking Distillation(RRD)
Distillation Experts(DE)
1. Expert for distillation
전문가를 활용해 교사의 hidden representation space에서 지식을 증류한다.
소규모 feed-forward network인 expert는 학생의 해당 중간 계층에 있는 표현에서 교사의 선택된 중간 게층에 대한 표현을 재구성하도록 훈련된다.
여기서 ht(⋅)을 교사 모델의 representation space( \( \in \mathbb{R}^{d_t} \)에 대한 매핑 함수로 표시한다.
hs(⋅)은 학생 모델의 매핑 함수이다.
전문가 E는 아래의 식을 통해 ( hs(u)에서 ( ht(u)를 재구성하도록 훈련된다.

KD 프로세스에서의 교사 모델은 이미 훈련됐고 frozen 되었기에 해당 방적식을 최소화 함으로써 학생 모델의 parameter와 전문가가 업데이트된다.

2. Expert selection strategy
단일 전문가만 사용할 경우, 다양한 엔티티의 지식을 모두 증류하도록 훈련하면 약한 상관관계가 있는 엔티티의 정보가 혼합되어 전문가에게 반영된다.
이는 학생 모델이 사용자의 선호도를 발견하는 것에 방해가 되므로 DE에서는 여러 전문가를 병렬로 배치하고, 각 전문가가 증류하는 지식을 명확하게 구분한다.
여기서 핵심은 교사의 지식을 기반으로 표현 공간을 독점적으로 나누고, 각 전문가가 해당 부분을 증류하는데 전문화되도록 하는것이다.
(Figure 2-(a))
여기서 동일한 분할에 속하는 표현은 서로 강한 상관관계를 가지며, 서로 다른 분할에 속하는 약한 상관관계와 혼합되지 않고 동일한 전문가에 의해 증류된다.
여기서 DE의 지식 전달은 두 단계로 이루어진다.

1. selection network는 먼저 증류할 지식에 대한 각 전문가의 specialization 정도를 계산한다.
2. 계산된 분포를 기반으로 전문가를 선택 후, 해당 전문가를 통해 지식을 증류한다.
여기서는 M명의 전문가 E1,E2,…,EM과 출력이 M차원 벡터인 selection network S가 있다.
사용자 u의 지식을 교사로부터 증류하기 위해 S는 정규화된 specialization score vector \( \alpha^u \in \mathbb{R}^M \)을 아래의 식을 통해 계산한다.

이후, 계산된 분포를 기반으로 전문가를 선택하고, 이때 selection variable su는 증류 ht(u)를 위해 선택할 전문가를 결정한다.
이는 M-차원 one-hot vector이며 전문가가 증류를 위해 선택될경우 1로 설정된다.
DE는 \( \alpha^u_m \)로 매개화된 multinoulli distribution ( p(sum=1|S,ht(u))=αum에서 su를 샘플링한다음 교사의 표현을 아래의 식을 통해 재구성한다.
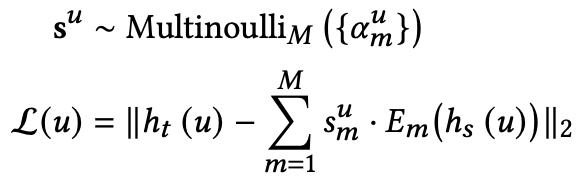
DE는 Gumbel-Softmax를 사용하여서 one-hot selection variable su를 얻고, 다음의 식으로 교사의 표현을 재구성한다.
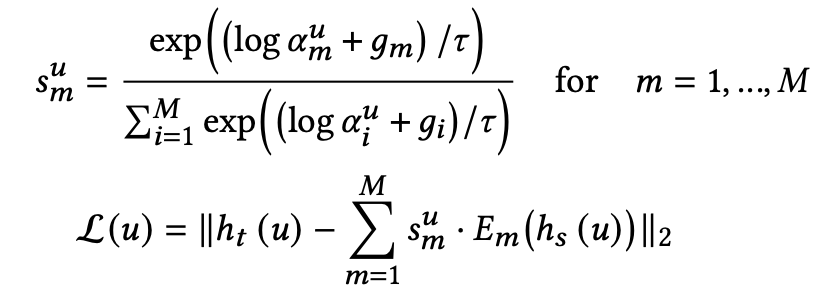
여기서 gi는 Gumbel(0, 1) 분포에서 가져온 i.i.d(독립항등분포)이며, relaxtion의 정도는 temperature paramter τ에 의해 제어된다.
여기서 저자는 expert selection이 교사의 지식을 기반으로 하기 때문에 교사의 representation space의 엔티티 간 상관관계가 전문가 선택에 자연스럽게 반영되기 때문에 강한 상관관계가 있는 엔티티 지식만 증류하도록 훈련받아 더 나은 지침을 제공할 수 있다고 언급했다.
또한 여기서 한명의 전문가를 선택하는 것 대신 attention mechanism을 사용해도 된다고 하는데, CF 지식을 증류하기 위해서는 expert selection이 더 적합한 선택이라고 한다.
그 이유는 attention의 경우, 각 개체의 지식을 증류하는데 관련된 모든 전문가를 만들기 때문이라고 하면서 section 5.3에서 실험을 통해 이를 주장하고있다.
Optimization of DE
DE의 최적화는 기본 모델의 loss function과 공동으로 최적화된다.
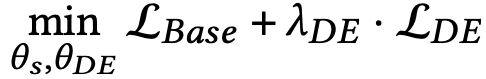
θs는 학생 모델의 learning paramter, θDE는 DE의 효과를 제어하는 hyper-paramter이며 전문가는 추론 단계에서는 사용되지 않는다.
여기서 base model은 기존의 Recommender(BPR, NeuMF)가 될 수 있다.
Relaxed Ranking Distillation(RRD)
여기서는 item 간 순위 순서를 직접 고려하여 교사의 예측에서 드러난 지식을 증류하는 새로운 방법 RRD를 제안한다.
여기서는 교사 모델의 추천 목록가 학생 모델의 순위 일치 문제로 문제를 공식화한다.
하지만 목록별 loss를 채택하는 것만으로도 순위 결정에 부정적인 영향을 미칠 수 있다.
그 이유는, 사용자는 많은 아이템 중에서 몇개의 아이템에만 관심이 있기 때문에 관찰되지 않은 모든 항목의 세부 순위를 학습시키는 것은 어렵고 효과적이지 않기 때문이다.
그러나 교사 모델의 추천 목록엔 관찰되지 않은 아이템에 대한 잠재적인 선호도에 대한 정보가 포함되어있다.
(사용자가 관심을 가질만한 아이템은 상단에, 관심을 갖지 않을 아이의 대부분은 상단에서 멀리 떨어져있다)
이 정보를 바탕으로 RRD에서는 모든 순위를 학습하기보단 이보다 완화된 순위 매칭 문제를 다룬다.
RRD에서는 흥미로운 아이템 중 세부 순위 순서를 무시하고, 교사의 추천 목록과 학생의 추천 목록을 일치시키는 것을 목표로 한다.
즉, 증류시키는 정보는 다음과 같다.
- 흥미로운 아이템 중 세부 순서 순위
- 흥미로운 아이템과 흥미롭지 않은 아이템 간 상대적 순위 순서의 정보
RRD의 전체적인 그림은 Figure 2.(b)를 참고하자.
1. Sampling interesting/uninteresting items
해당 단계에서의 첫번째 작업은 교사 추천 목록에서 item을 샘플링하는 것이다.
여기서 흥미로운 항목과 흥미롭지 않은 항목을 K,L 이라고 한다.
흥미로운 항목을 샘플링하기위해서는 순위 목록에서 높은 위치에 더 중점을 두는 ranking position importance scheme를 채택했다.
이를 통해 RRD는 교사가 예측한 각 아이템에 대한 순위에 대해 사용자의 잠재적 선호도에 따라 흥미로운 항목을 샘플링한다.
2. Relaxed permutation probability
이후, RRD는 Relaxed permutation probability를 정의하고, 사용자 u를 위해, πu는 교사의 추천 목록에서 샘플링된 모든 항목의 순위 목록을 원래 순서로 정렬된 형태를 나타낸다.
ru는 학생 모델에 의해 예측된 샘플링된 아이템의 순위 점수를 나타내며, 완화된 순열 확률은 아래의 식과 같다.
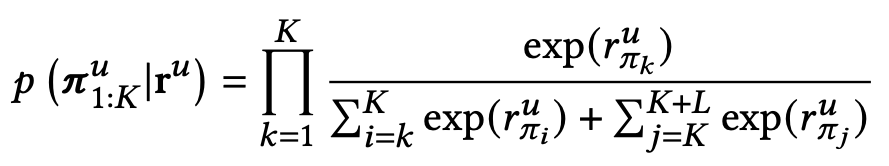
여기서 r_^u_{\pi_i}는 πu에서 k번째 아이템에 대해 학생이 예측한 순위 점수이며, \pi_^u_{1:K}는 흥미로운 아이템을 포함하는 부분 목록을 의미한다.
RRD는 모든 사용자에 대해 log-likelihood log p(π1:K|r)을 최대화하는 방법을 학습하며, 이를 통해 학생 모델은 흥미로운 아이템 중 교사의 추천 목록에서 세부 순위 순서를 유지하면서, 추천 목록에서 L보다 높은 K를 찾도록 학습된다.
3. Optimization of RRD
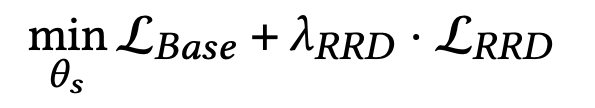
θs는 학생 모델의 learning paramter, θRRD는 RRD의 효과를 제어하는 hyper-paramter이다.
Optimization of DE-RRD
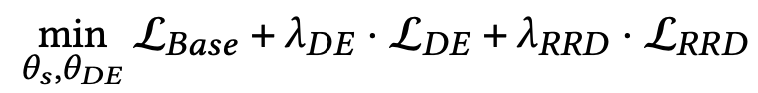
DE와 RRD의 optimization을 합친 식으로 해당 식을 통해 최적화가 진행된다.
Experiments
- Dataset: CiteULike, Foursquare
- Base Models: BPR, NeuMF
- Teacher/Student
: 성능 별 추천이 더 증가하지 않을 때까지 학습, 성능이 가장 좋은 모델을 교사 모델로 사용함
: learning paramter의 수를 제한하여 세가지 학생 모델 구축함 - Evaliation protocol
- Hit ratio(H@N)
- Normalized discounted cumilative gain(N@N)
- Mean reciprocal rank(M@N)
- N@N과 M@N은 상위 순위의 hit에 더 높은 점수를 할당하는 위치 인식 순위 측정 지표이다.
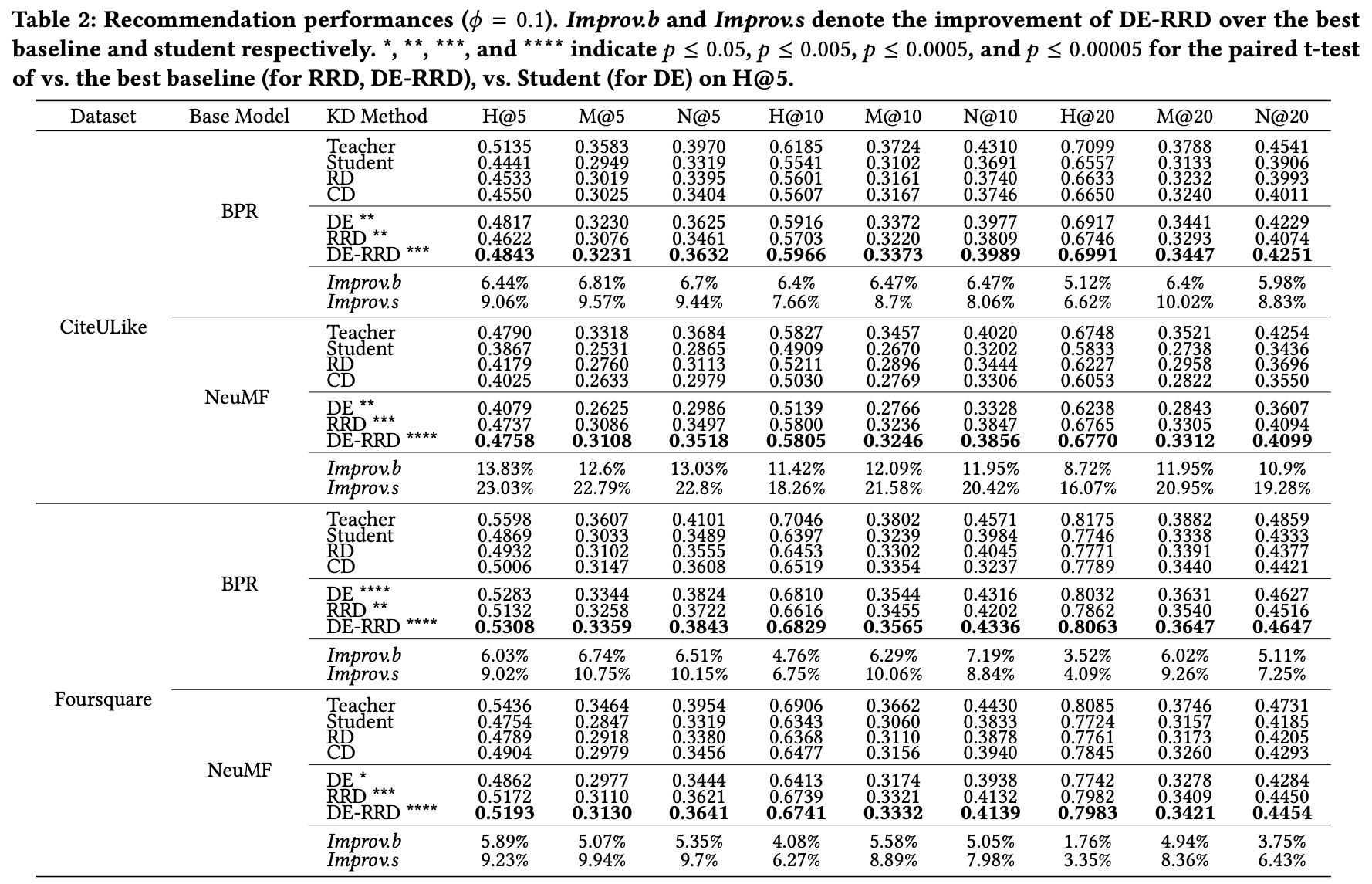
DE-RRD가 다른 모델에 비해 성능이 좋음을 보인다.
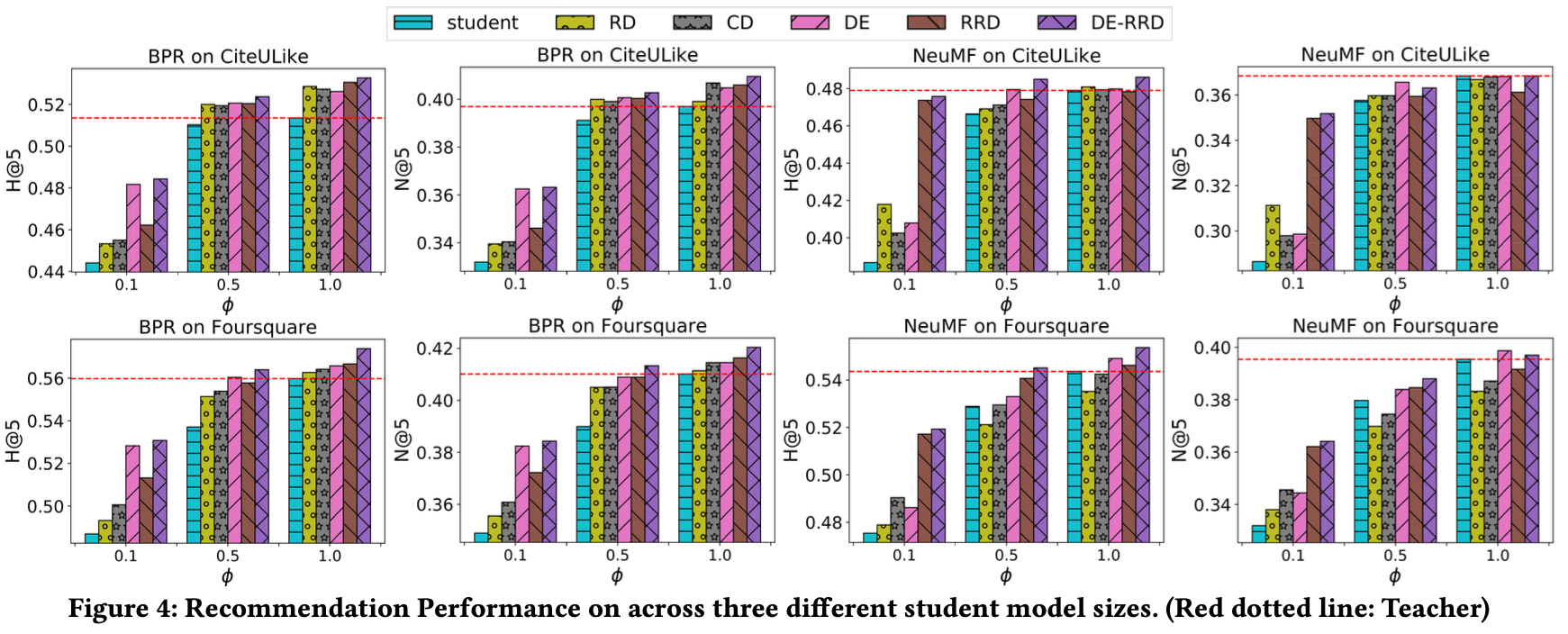
여기서 ϕ=1은 학생 모델과 교사 모델이 동일한 구조를 가지는 것을 의미하는데 이때 성능이 가장 좋게 나왔다.
이를 통해 기존의 Recommender를 극대화하는 데도 사용될 수 있다는 것을 보여준다.
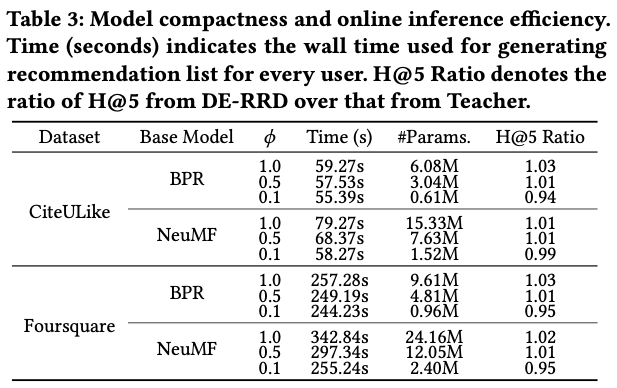
여기서는 'Tesla P40 GPU and Xeon on Gold 6148 CPU' 해당 사양으로 pytorch를 돌렸을 때 시간을 나타내는데 학생 모델이 교사 모델에 비해 학습 파라미터가 10-50%에 불과하지만 비슷한 성능을 달성하는 모습을 볼 수 있다.
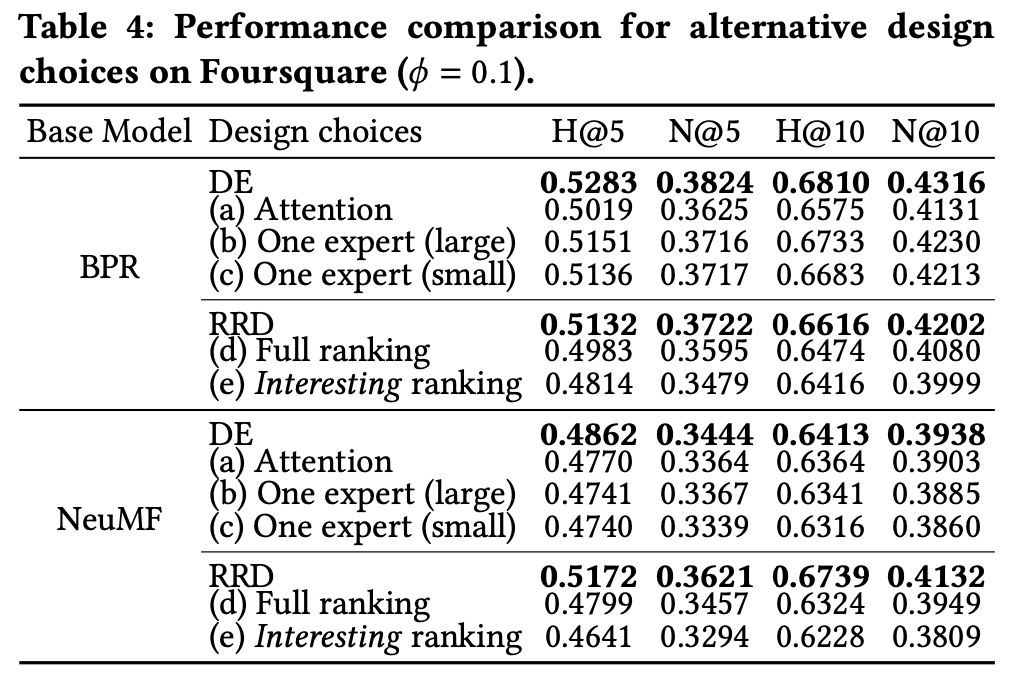
여기서는 DE 파트에서 언급한 attention에 대한 실험 비교가 나오는데, 일단 (a)는 attention을 사용했을 때, (b)는 한명의 큰 전문가를 사용, (c)는 한명의 작은 전문가를 사용했을때의 결과를 나타낸다.
여기서는 expoert selection을 사용한 DE가 성능이 가장 좋음을 보였다.
또한 RRD의 경우 (d)는 샘플링된 모든 아이템에, (e)는 상위 순위 아이템(interesting item)에 완화를 적용하지 않은 목록별 손실을 적용한 경우의 결과를 나타낸다.
보면 목록별 손실을 적용한 것 자체만으로도 순위 결정에 부정적인 영향을 나타내며,
(d)는 모든 항목 중 전체 순위 순서를 일치시키는 방법을 학습하며, (e)는 흥미로운 아이템과 흥미롭지 않은 아이템 간 상대적 순서를 고려하지 않기 때문에 흥미로운 항목의 순쉬가 맨 위에서 멀리 밀려난 것이다.
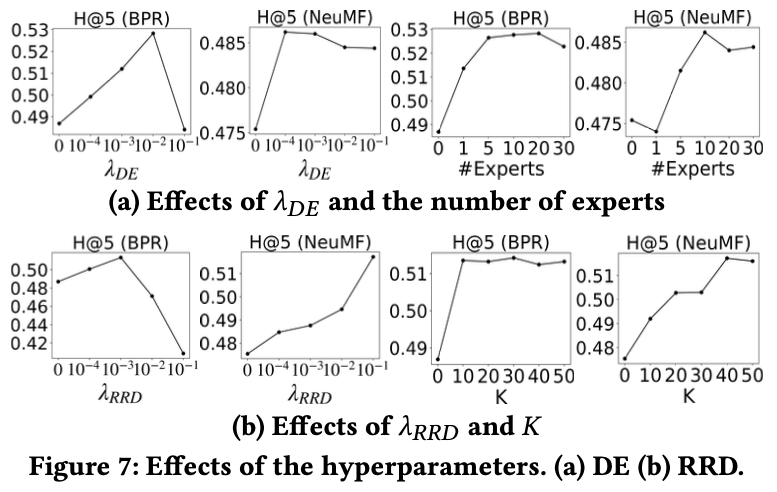
(a)는 λDE와 전문가의 수의 영향력에 대해 보여주는 그래프이며, (b)는 λRRD와 아이템의 수 K의 영향력을 보여주는 그래프로, 전문가의 수와 K의 경우, 10-20명과 30-40명 근처에서 가장 높은 성능을 보였다.
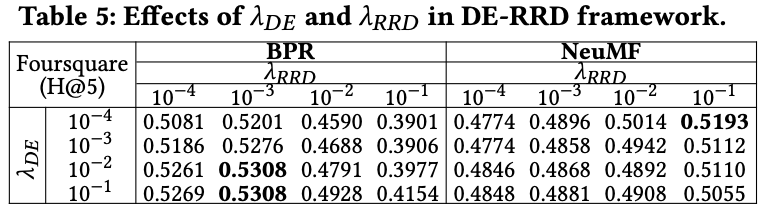
여기서는 λDE와 λRRD의 조합의 효과를 보여주고, 일반적으로 DE-RRD의 최상의 성능은 각 방법이 최상의 성능을 달성하는 범위에서 관찰됐다.
